Conceitos básicos da matemática
Breve história dos números I


/pt/conceitos-basicos-da-matematica/a-joia-dourada-da-matematica/content/
Em , perto de onde o rio Nilo nasce, Jean Heinzelin de Braucourt descobriu um pequeno osso com mais de anos. Além de ser bem antigo, este ossinho é testemunha de um dos maiores feitos intelectuais do homem: o conceito de número. Este objeto é conhecida como"osso de Ishango", por conta do nome da região Africana onde ele foi encontrado. Nele estão talhadas uma série de cortes agrupados de tal modo que revela uma compreensão numérica que vai além de uma simples contagem.

Este foi o começo dos números, e de simples marcas em ossos de animais pré-históricos, se tornaram uma das ferramentas mais poderosas da humanidade. Mas como eles se desenvolveram e em quais circunstâncias? Aqui descobriremos isso e muito mais.
Há uma antiga tribo na Austrália Central, os Warlpiri, que praticamente não possui o conceito de número. Eles usam duas palavras para representar quantidades "sozinho" e "muitos". Quando se pergunta a um idoso quantos netos ele tem, ele simplesmente diz o nome de cada um e no final "muitos".
Como é possível que um povo com mais de anos de história não tenha desenvolvido mais conceitos numéricos? Por outro lado, os antigos povos do oriente como os sumérios ou os chineses desenvolveram não apenas números, mas métodos aritméticos que deixaram sua marca até os dias de hoje.
Esta diferença em relação ao desenvolvimento da criação matemática está associada ao surgimento de grandes cidades ou centros urbanos. Isso porque nesses locais é necessário organizar, armazenar e distribuir alimentos, além de ter uma ideia do número de habitantes e recolher impostos.
Os babilônios, por exemplo, usavam um sistema de escrita chamado cuneiforme. Eles representavam as unidades com cunhas e desta forma simbolizavam os números de ao . Para representar o número dez usavam uma cunha colocada horizontalmente. Para escrever os números do até o estes dois símbolos eram suficientes.

O era um número muito especial para eles e era a base do seu sistema numérico. Este número traz suas vantagens, porque é o menor número divisível por , , , e além de ter também como divisores o , , , e . Isto sugere que ele não foi escolhido por acaso, mas sim por conta das suas propriedades, o que nos faz pensar que os babilônios tinham um grande domínio da aritmética.
Este povo deixou sua marca até hoje: observe por exemplo, que dividimos as horas do dia em minutos, e um minuto por sua vez, possui segundos. A mesma coisa acontece com a medida dos graus de uma circunferência, que tem no total , que é , cada um desses graus é dividido em minutos e cada minuto em segundos e isso graças aos babilônios.
Por outro lado, os egípcios usavam representações um pouco menos funcionais, mas também fizeram grandes contribuições para o desenvolvimento dos números. Eles usavam um sistema em que cada símbolo representava dez vezes mais que o anterior:
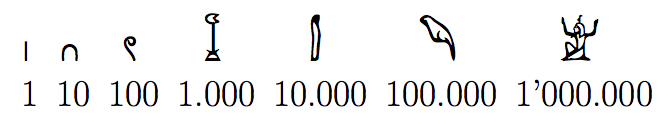
Para representar quantidades colocavam estes símbolos juntos e o valor de cada um era somado, conforme a quantidade total. Para representar o por exemplo, usavam os símbolos mostrados na imagem abaixo.
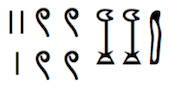
Uma das maiores contribuições dos egípcios para o desenvolvimento dos números foi as frações, mas eles só representavam as que tinham o um como numerador, exceto o e , que eram usadas muitas vezes. A concepção deste tipo de números foi e é definitivamente um passo não só necessário, mas também base no desenvolvimento da matemática e na forma como entendemos o mundo.
Mas os avanços mais impressionantes foram realizados pelos gregos. Estes deram uma visão mais ampla ao conceito de números e da matemática em geral. Assim como seus predecessores, relacionavam os números com divindades e com a perfeição do universo. Tanto foi assim, que um grego quase ficou louco ao descobrir um novo tipo de número que não coadunava com sua postura religiosa, estamos falando de Pitágoras.
/pt/conceitos-basicos-da-matematica/breve-historia-dos-numeros-ii/content/